• Can relate aspects of the graph of a polynomial function to the coefficients

(for each team)
• Graphing calculator or spreadsheet program

Procedure: This activity is best done by students working individually or in teams of two.

Students will need to already understand how to enter a polynomial function into a graphing calculator or spreadsheet program.

You may wish to simplify the activity by restricting the investigation to third or fourth-order polynomials from the beginning.

Answers:

1. Change the “f” coefficient from “–10,000” to “–20,000.” What is the effect on the roller coaster? Why? The roller coaster drops to the right more steeply. “f” is the coefficient of the linear term, and when it has a negative value then that term imparts a negative slope to the graph. As f becomes more negative, that slope increases.

2. What do you think would happen if you changed “f” to “-30,000”? Try it and explain what happened. As above.

3. What happens if you change “f” to “0”? Explain. The graph climbs more strongly to the right.

4. Change all coefficients to “0” except for “d” (leave it at “20”). Describe the result. The result is a standard cubic function graph, increasing from left to right.

5. Now change “d” to “-20” (leaving all other coefficients equal to zero), and create the graph. Explain the results. This inverts the graph, causing it to drop from left to right.

6. Leave d = -20, and change “f” from “0” to “10000”. Try several other values of “f”, to see the effect. Describe the results. This will cause “humps” to appear in the graph.

7. Set “a” and “b” equal to zero, and see if you can find values for the other coefficients that produce a graph of this shape:

y = -14x⁴-40x³+10000x²+ 10000x + 300000

Polynomial Roller Coasters

The shape of a roller coaster could be modeled by a polynomial function, such as this one:

y = ax⁶ +bx⁵ + cx⁴ +dx³ +ex² + fx + g

Here is an example:

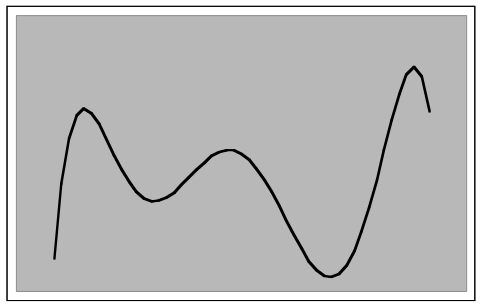
y =-.015x⁶ +.01x⁵ + 14x⁴ +20x³ -3000x² -10000x + 300000

(Domain: -25≤x≤25)

Use a graphing calculator or spreadsheet program to investigate the effects of the coefficients on the shape of the roller coaster, as follows:

1. Change the“f” coefficient from “–10,000” to “–20,000.” What is the effect on the roller coaster? Why?

_______________________________________________________

_______________________________________________________

_______________________________________________________

2. What do you think would happen if you changed “f” to “-30,000”? Try it and explain what happened.

_______________________________________________________

_______________________________________________________

_______________________________________________________

3. What happens if you change “f” to “0”? Explain.

_______________________________________________________

_______________________________________________________

_______________________________________________________

4. Change all coefficients to “0” except for “d” (leave it at “20”). Describe the result.

_______________________________________________________

_______________________________________________________

_______________________________________________________

5. Now change “d” to “-20” (leaving all other coefficients equal to zero), and create the graph. Explain the results.

_______________________________________________________

_______________________________________________________

_______________________________________________________

6. Leave d = -20, and change “f” from “0” to “10000.” Try several other values of “f”, to see the effect. Describe the results.

_______________________________________________________

_______________________________________________________

_______________________________________________________

7. Set “a” and “b” equal to zero, and see if you can find values for the other coefficients that produce a graph of this shape: