• Square root
• 45-45-90 triangle

• Can apply the Pythagorean Theorem in real world situations
• Can use the problem-solving strategy, “Make a model.”

Procedure: Distribute the handout to students working in teams of two or three, and ask the teams to study it and talk it over for a few minutes. Then, as a class discussion, ask students to summarize the problem, so that it’s clear to everyone what they are being asked to do.

Next, ask students to think about the strategies they could use to solve this problem, and guide the class to agreement that a good strategy would be to make a model. Provide each team with supplies (paper, a ruler, scissors, a compass) with which they can create a model of the lawn (with one rectangular piece of paper, for example 10” x 5”), and the sprinkler coverage areas (with about 10 circles of proportionate size: if the lawn is 10” x 5,” each circle would have a radius of 1”).

Students should discover that one method of covering the lawn with sprinklers with relatively waste is by placing them in a rectangular array, like this:

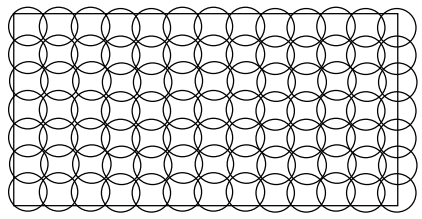
The application of the Pythagorean theorem to the 45-45-90 triangles, indicated in the diagram, below leads to the results that:

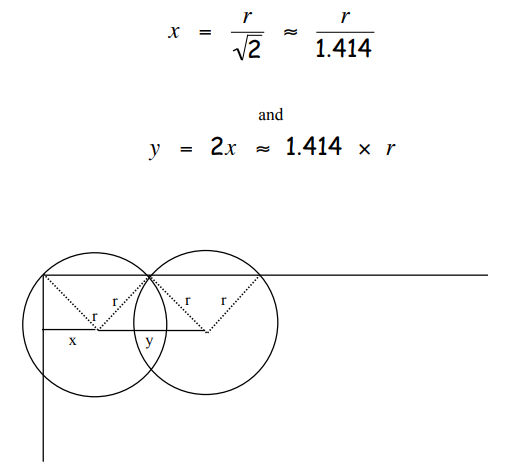
Water Geometry

Below is a plan for a suburban park. It includes a large rectangular lawn that is 200 feet long and 100 feet wide.

It is your job to install the water system, using sprinklers that shoot water jets in a circular pattern to a distance of 20 feet.

The sprinkler installation instructions recommend placing the sprinklers as follows:

1. Place the first sprinkler in the top left corner of the lawn, at a distance of 20 ÷ 1.414 feet from each edge.

2. Place remaining sprinklers in a rectangular grid, separated from each other by a distance of 20 × 1.414 feet.

Can you explain where the number “1.414” comes from in these instructions?