• Sample
• Population

• Can solve multi-step problems
• Can apply the problem-solving strategy, “Solve a simpler problem”
• Can interpret data in a chart or table
• Can use proportional thinking to solve problems

Procedure:

Distribute the handout to students working in teams of two or three, and ask the teams to study it and talk it over for a few minutes to try to summarize the problem that is presented. (You may wish to start this off with a class discussion so that all students understand the nomenclature and what the tables mean.)

Explain to students that this is a complicated problem, and that one good strategy when faced with a complicated problem is to try to break it into smaller parts and solve one of those parts. In this case, tell them that you want them to first find the total volume of three trees that were measured to have an 8” dbh and 20 foot height.

You may wish to have students solve this in teams or as a class activity. (Answer: Use the second table to find that the volume of one such tree is 21 board feet, multiply to determine that the volume of those three trees together is 63 feet.)

Now ask the teams to work out how they would find the total volume of all of the sampled trees, and write that out (they do not actually need to carry out the computations, they need only describe how it would be done: by multiplying the number of trees in each table position in the top table by the corresponding volume of those trees in the bottom table).

Finally, ask the teams to work out how they would use that answer to determine the volume of all 1000 trees in the stand. (Multiply by 20, since the sample is 1/20 of the size of the population.) In discussing this, introduce or review the concepts of sample and population in this context. You may also wish to use this opportunity to review the importance of choosing a representative sample in this case, and how a non-representative sample could cause a poor estimation of total volume.

Timber Cruise

To: Forestry Teams
Regarding: Volume Calculation

We recently completed a cruise1 of 50 acres of pine trees in one of our Oregon forests. As usual, we measured the heights of the trees and their diameters at a point 4.5 feet above the ground (“diameter at breast height”, or “dbh”).

We sampled 50 out of the 1,000 trees that are on that lot, with these results:

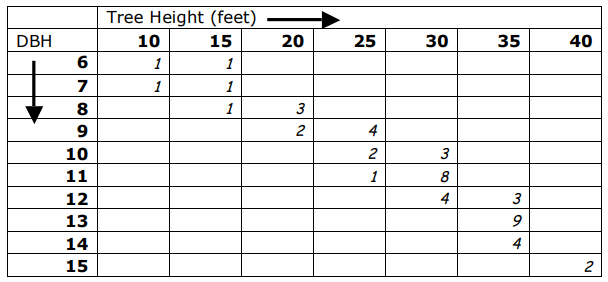
The number in each box indicates how many trees were found with the indicated dbh and height values for that box. (For example, there were 3 trees with a dbh of 8 inches and a height of 20 feet.)

This table shows the volume of wood, in board feet, that is found in a tree with a certain dbh and height:

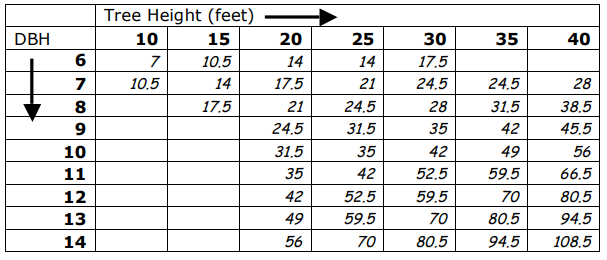
Can you tell us how to use this data to get an accurate estimate of the total volume of wood that is on that lot?

¹ Timber cruise: inspection of a timber stand made to estimate volume, quality and value of trees.