· Rational expression

· Can solve equations involving rational expressions
· Can plot a rational function

Pencils, paper clips

Procedure: This project should be done by students individually or in teams of two.

Distribute the handout and discuss the two diagrams on the first page. Ensure that students understand all of the parts of the equation at the bottom of the page. Elicit or present the fact that this equation involves a rational expression, and ensure that students understand what is meant by the term “rational expression”.

Answers:

1.

2.

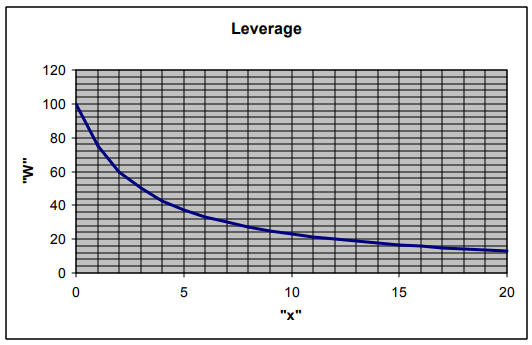
a) As x gets larger, the weight being lifted moves farther and farther from the point of support, which means more force is required at that point.

b) When x is 0, the weight is located exactly at the point of support, and so all of the lifting force of 100 pounds is being applied directly to the weight, which can therefore be 100 pounds.

To: Research Dept
From: Head of Physical Therapy

One of the things the I think our clients may not understand very well is the amount of force that a muscle like the biceps has to exert in order to actually lift something. Some research on this would also help us in developing new therapies for handling injuries.

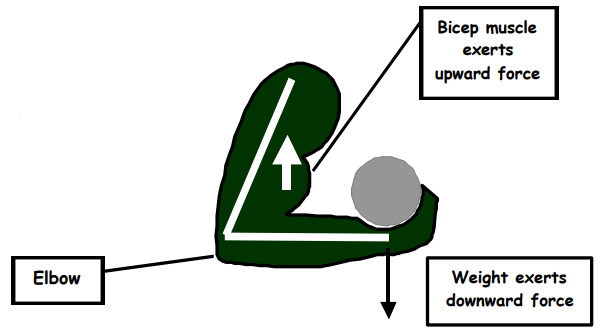
This diagram shows how the biceps muscle is used to lift a weight.

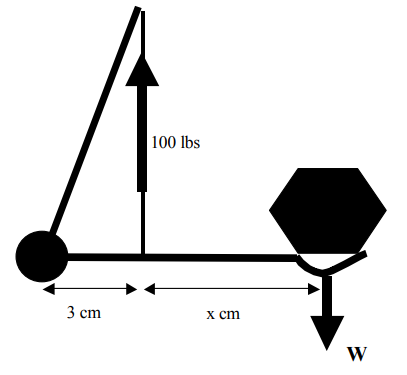
This diagram presents a model of the above situation. If the supporting “biceps” exerts a force of 100 pounds, and the point of support is 3 centimeters from the “elbow”, as shown, then the amount of weight that can be lifted is related to the distance “x” by this equation: W = 300/(3 + x)

I would like you to use the model make some calculations, as follows:

1. Find “W” for these values of x: 0 cm, 1 cm, 3 cm, 9 cm, 12 cm.

2. Plot this function for the range of x = 0 to x = 20 centimeters.

a. What happens to the amount of force that can be lifted as x gets larger? Why do you think that would be that way?

b. Explain the value of W when x = 0.

Please give me a report that explains exactly how you answers these questions, and is clear enough for our clients to read and understand.

Thanks,

A.S.