• Angular separation

• Can solve an equation involving a trigonometric ratio.
• Can perform operations with numbers written in Scientific Notation

Procedure:

Prepare for presentation the Futures Channel Movie “The Starshade.” Tell students that as they watch the movie, you want them to think about this question (which should be posted):

Why would it be difficult to see planets that are orbiting around distant stars?

Watch the movie once, straight through. At the conclusion, give students a minute to think about the question again, and share some answers. Guide the discussion to class agreement on these two answers:

1) The light from the star is much brighter than the light from the planet.

2) The star and planet are so far away that they will appear to be very close together.

Explain to students that even though the Starshade can solve the first difficulty, the second difficulty remains, and this limits the distance at which planets might be seen even with the shade.

Depending on the level of your class, you may wish to use the attached handout as an outline for your own explanation of this situation, or ask students to study it independently or in small groups. In either case, the two problems will help you assess their understanding, as well as their ability to solve this real-world trigonometric ratio problem.

You may choose to work through one of the problems with the class, and/or assign the problems as group work or as a homework or extra-credit assignment.

Problem #1 answer: About 200 million miles.

Problem #2 answer: 1.06 x 10¹⁴ miles, or about 18 light years.

Stars and Planets

Imagine you are standing on the side of the highway at night, watching a car approach. When the car is far away, it seems to be one bright light. As it gets closer, you can see that the one light is actually two headlights.

This is because, when the car is far away, the light from the two headlights is coming at you from almost the same direction. Here is how that looks from above:

As the car gets closer, the headlights seem to move farther apart. Of course, the distance between the headlights doesn’t change, but they seem farther apart because the light beams are now coming to you from different directions:

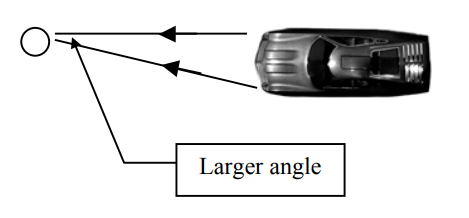
If you study these diagrams, you will see that your ability to see that there are two headlights depends on the angle between the two beams of light when they reach your eyes. Study the diagrams more closely and you will see that the size of that angle depends on two things:

a) How far away the car is

b) How far apart the headlights are

To find the angle, you would use this equation:

In the same way, when a telescope is looking at a distant star and planet, they can only be seen as separate objects if the angle between the light from the star and the light from the planet is large enough.

Test your understanding of the above by solving these two problems:

1) A star is 10 light years away from the Solar System (5.8 x 10¹³ miles). If a telescope requires an angular separation of .0002 degrees to see a nearby planet as a separate point of light, how far away from the star would the planet have to be in order to be seen?

2) Suppose a telescope requires an angular separation of .00005 degrees to see a star and planet as two separate objects. What is the greatest distance at which it could see a planet which is orbiting at a distance of 93 million miles from its sun?