Mathematics
Grade Levels: 7th Grade, 8th Grade, 9th Grade, 10th Grade, 11th Grade, 12th Grade,
Topics: Geometry (Circles)Geometry (Right Triangle)Geometry (Theorems)
Common Core State Standard: G-MG.3,
Concepts:
• Circumference
• Intersect
• Theorem
• Right Triangle
• Tangent
• Can apply geometric theorems in a problem-solving situation
• Can create an equation based on verbal description of the relationships of variables
• Can find the length of one of the sides of a right triangle, given the other two
Lesson:
Procedure: Prepare for presentation the Futures Channel movie, Building and Testing Wheels. Tell students that as they watch the movie, you want them to think about this question (which should be posted):
What geometric concepts can you identify in this video?
At the end of the movie, have students take a minute or two to write down their answers to the question, then share them. Make a list of the answers on the board, and ensure that it includes at least these items:
Circle
Line segment (spoke)
Circumference (of the wheel)
Angles
Intersection (where the spoke meets circumference of wheel)
Note: If a student suggests “radius”, meaning the spoke of the wheel, add it to your list, but make the comment that “We’re going to take a closer look at this.”
Tell students that the spoke of a bicycle wheel is actually an interesting geometry problem, and arrange them into teams of 3 students each and distribute the handout.
As a class, read the handout through the statement of the problem (about halfway down the page). As you do so, discuss the arrangement of the spoke to make sure it is clear to everyone that the spoke is not actually a radius, since it does not end at the center of the wheel, but rather on the outside of the hub.
Ensure that students understand the problem they are being asked to solve.
Depending on the prior knowledge and ability level of your class, you may wish to have teams work on their own to use the information at the bottom of the page to solve the problem, or first continue working as a class to review the definitions and theorems and ensure that they are understood, then have them work in teams to solve the problem.
This is also a good opportunity to ensure that students understand what a theorem is.
As the teams work, circulate and ask questions to ensure that they really do understand the definitions and theorems, and help them as needed. If a team seems at a loss as to how to approach the problem, you may wish to suggest that they apply the geometry problem-solving strategy of “look for or create triangles”, or, if that’s not enough of a hint, suggest that they create the triangle consisting of the spoke, the wheel radius, and the radius of the hub, as shown here:
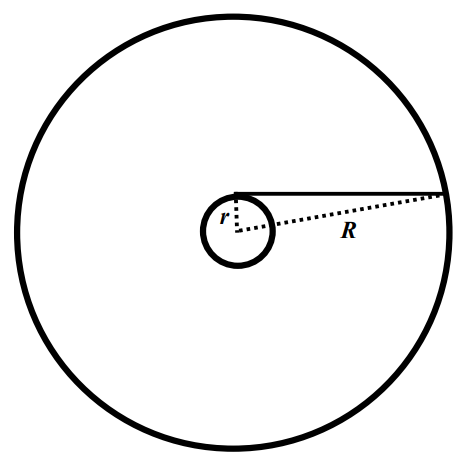
With this triangle in view, ask students to
• apply the first definition (and observe that the spoke is tangent to the hub),
• then apply the second theorem (observing that the angle of intersection of the spoke with hub radius is 90 degrees),
• then apply the second definition (observing that the triangle is a right triangle, with the radius of the wheel as the hypotenuse).
The first theorem (Pythagorean Theorem) is then applied to generate this formula (where s is the length of the spoke):
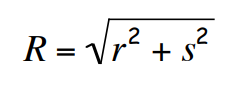
This is the equation that can be solved to find s, if R and r are known.
Spoke Math
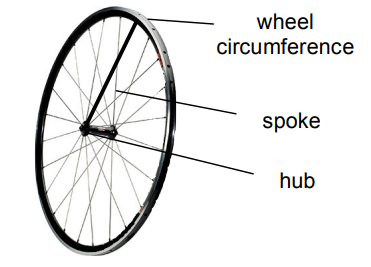
The spoke on a bicycle wheel extends from the circumference of the wheel to a point on the hub of the wheel, as shown in this diagram:
For this problem we are going to make two assumptions:
1) Imagine that our bicycle wheel is flat, rather than 3-dimensional.
2) Assume that the spoke is connected to the hub in such a way that the line of the spoke intersects the hub at only one point:
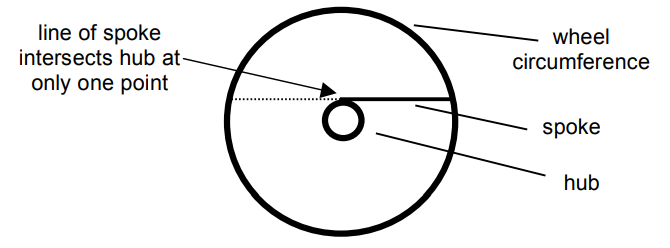
If you know the radius of the wheel (R), and the radius of the hub (r), how can you find the exact length of the spoke?
Here are some geometric definitions and theorems that might help:
1) Definition: A line which intersects a circle at only one point is said to be tangent to the circle.
2) Definitions: A right triangle is a triangle with a 90-degree angle. The longest side is called the hypotenuse, the shorter sides are called legs.
3) Theorem: The length of the hypotenuse of a right triangle is equal to the square root of the sum of the squares of the lengths of the legs.
4) Theorem: The angle between a line that is tangent to a circle and a radius of that circle that intersects the tangent line at the point of its intersection with the circumference of the circle is always 90 degrees.
