Mathematics
Grade Levels: 4th Grade, 5th Grade, 6th Grade, 7th Grade,
Topics: Geometry (Circles)
Common Core State Standard: 7.G.4,
Concepts:
· Diameter
· Circumference
· π
· Understands and can apply the formula “circumference = π x diameter”
Materials:(for each team):
· Four cans of different diameters (on three of the cans you should use a marker to draw in a diameter, and these should be labeled as cans “#1”, “#2”, and “#3”)
Lesson:
Procedure: This activity can be done in teams of two or three students.
What the students are actually measuring is the circumference of the cans, which is equal to the rolling distance for one complete revolution. The quotient of rolling distance divided by diameter, then, should be approximately p (about 3.14).
For the fourth can, the task becomes to find a diameter, d, such that when the circumference is divided by that number, the result is approximately p. Guess and check is a good strategy for solving this problem for elementary students.
If the quotient for any of the three cans is very different than the other two, have the students make that measurement again.
Rolling Cans
1. Get four cans of different sizes.
2. Draw a long straight line on a piece of paper . Choose one can, and make a mark somewhere on the edge of the top of the can. Lay the can down on the paper with the mark on the line. Make a mark on the line next to the mark on the top of the can.
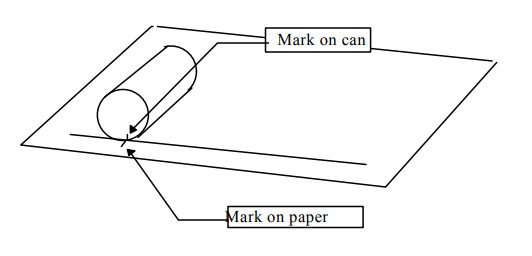
3. Roll the can so that its top travels straight down the line. Stop when the mark on the can has rolled all the way around to the bottom again. Make another mark on the line at that point. Measure the distance on the line between the two marks.
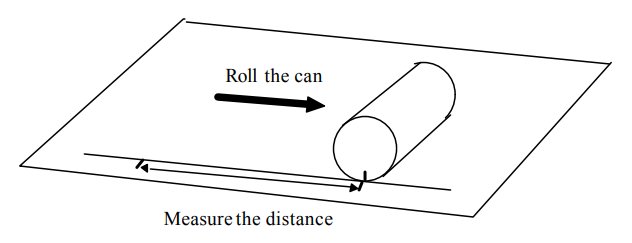
4. Measure the length of the diameter of the can. (This is the longest distances across the can.) Put the information you have into the chart on this page.
5. Divide the rolling distance by the diameter.
6. Repeat steps 2 to 5 with two other cans of different sizes.
7. What pattern do you notice?
8. Measure the rolling distance for another can, of a different size. Use the pattern to find its diameter.
| Rolling distance | Diameter | Rolling distance divided by diameter |
|
| Can #1 | |||
| Can #2 | |||
| Can #3 | |||
| Can #4 |
