· Can plot a point in a two-dimensional coordinate system, given the coordinates, or determine the coordinates of a given point
· Can extrapolate a graph when a pattern exists

Procedure: This activity is best done by students working individually or in teams of two.

The relationship between intensity of light (I), and distance from the source of the light (d), is given by the equation

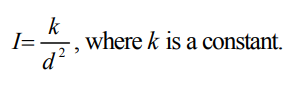
As the first step of their investigation, students should identify the two variables involved (intensity, measured in dots per square inch, and distance from the source of the light, measured in feet).

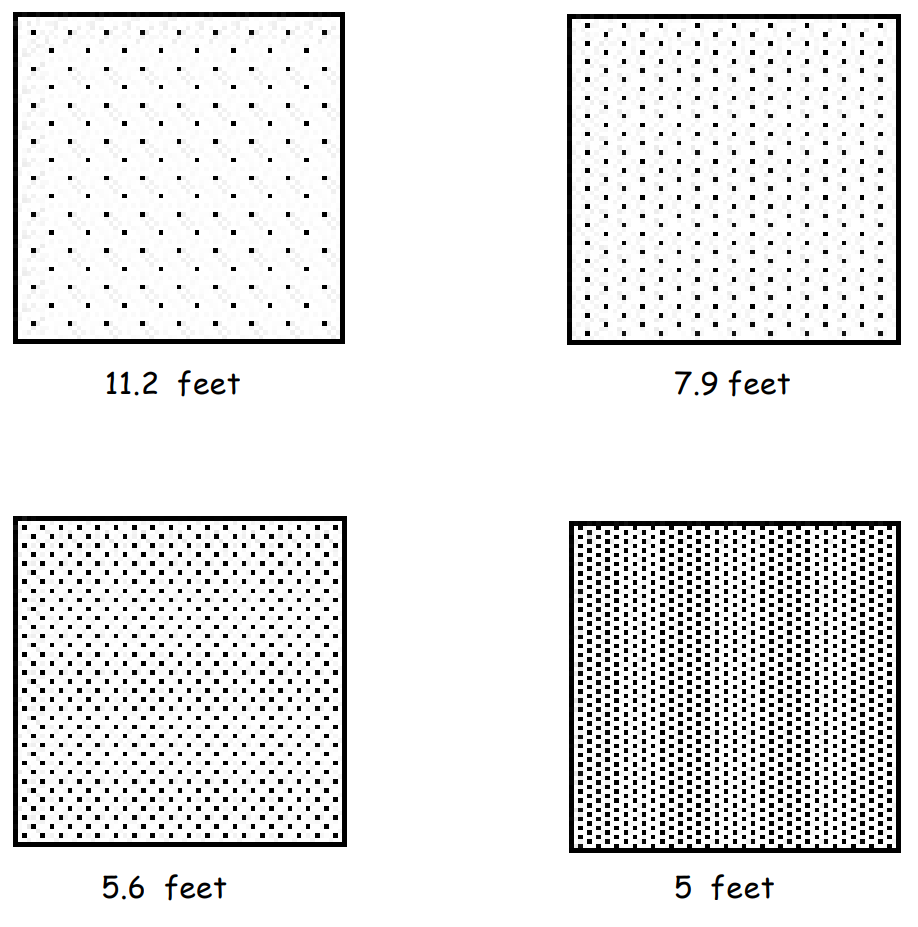
The next step would be to identify which is the independent variable (distance), and the dependent variable (intensity), and graph the four given data points in a cartesian coordinate system (11.2, 36.25), (7.9,72.5), (5.6,145), (5,181.25).

Beginning algebra students would sketch a curve in the graph to estimate the answers to the questions. Once they have done this you may wish to show them the equation (in this case, k = 4531.25) and have them plug in the four given data points to test the equation.

For more advanced students, you may wish to give them the general form of the equation, above, and have them determine the value of k and find the specific equation, or have the students themselves use trial and error to determine the general form of the equation (by testing equations such as I = -kd + c, I = k/d, I = k/d².

Answers: 10 feet corresponds to 45.3 dots per square inch; 3 feet would correspond to 503.5 dots per square inch.

Light Intensity

Investigation

The four images below represent the intensity of light at various distances from a flash bulb. The intensity is indicated by the number of dots per square inch.

What would the intensity be (in dots per square inch) at a distance of 10 feet from the flash? 3 feet?