Mathematics
Grade Levels: 6th Grade, 7th Grade, 8th Grade, 9th Grade, 10th Grade, 11th Grade, 12th Grade,
Topics: AlgebraDecimalsStatisticsGeometryPercentsFunctionsRatiosPatterns
Common Core State Standard: 6.RP.3, 6.SP.5c, 7.RP.3, 8.G.1,
Download the Teacher Guide PDF
Lesson:
Background: The ocean is host to an astonishing variety of plants and animals, including the algae which is the basis of the food chain for all of the other ocean life forms. Ninety percent of the ocean’s denizens live in the 100 meters closest to the surface, where there is much more light, and oxygen, than farther below. But some of the most fascinating creatures have somehow adapted to live in the cold, dark depths. How they do so is a
question that has intrigued biologists and naturalists for hundreds of years. Only recently, with the development of remotely operated vehicles that can withstand extremely high pressures, have we had the means to find an answer.
Curriculum Connections:
Decimals, Statistics
An important characteristic of seawater is the amount of oxygen that is present in the water, known as “dissolved oxygen”. It is measured in units of “milliliter of dissolved oxygen per liter of water”. For example, if you took 5 milliliters of oxygen and mixed it with 1 liter of water, the dissolved oxygen measure would be “5 milliliters per liter”.
This data shows the dissolved oxygen measured on a dive to a depth of 48 meters. Depth is measured in meters. Answer these questions:
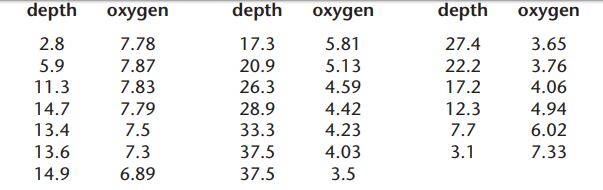
a) What are the average and range of the dissolved oxygen at the depths between 0 and 10 meters? At depths between 20 and 30 meters?
b) What would you expect the dissolved oxygen to be at a depth of exactly 25.0 meters? 45.0 meters?
 Geometry (symmetry, angles)
Geometry (symmetry, angles)
We usually think of symmetry as meaning that a line can be drawn through an object in such a way that the two sides can be folded over on each other to match perfectly. Actually, however, that’s only one type of symmetry, called “reflection symmetry”. Another type of symmetry is rotational symmetry, in which an object can be turned through a certain angle in such a way that it looks identical to the way it looked before it was rotated.
This starfish has rotational symmetry. What is the measure of the angle by which you could rotate it and have it still look just the same? Is there more than one angle for which that is true?
Percents
Light does not penetrate very deeply into the ocean, which is one reason why certain marine animals carry their own light. Suppose that, for every meter of depth, the intensity of light from the surface is reduced by 10%. If the intensity starts out at 1,000, at one meter below the surface it would be 900. One meter below that it would be 90% of 900, or 810. Find the intensity at 3 meters, 4 meters, etc. down to 10 meters of depth, and make a graph that shows your results.
Ratios, Algebra (patterns and functions)
Many forms of marine life have interesting geometric properties. Below are images of the shell of a chambered nautilus, which lives at a depth of roughly 600 meters. In the top three images, rectangles have been drawn in such a way that each side of the rectangle is tangent to a part of the shell’s spiral.

On the larger picture below, reproduce these rectangles, and draw as many more as you can. You should be able to draw a total of 6 rectangles. Then determine, for each rectangle, the ratio of the long side to the short side. What do you observe about this ratio as the rectangles get larger?

Investigating Buoyancy
Many marine organisms, including plants, are built in such a way as to take advantage of a force called buoyancy. In this activity you will investigate that force.
You will need these materials:
• Spring balance marked in grams
• Graduated cylinder (marked in milliliters)
• Thread
• A collection of objects which are narrow enough to fit into the cylinder and made of a variety of materials, such as bolts, screws, plastic pens, rulers, chalk etc.
Procedure:
a) Fill the graduated cylinder halfway with water. Note the amount of water, in milliliters.
b) Tie the thread around one of the objects tightly. (If you are using chalk, put a notch in it to hold the thread.) Tie the other end of the thread into a loop, so that there are about 15 centimeters of thread between the object and the loop.
c) Hang the object vertically from the spring scale and note the reading. This gives you the weight of the object, expressed in grams (as well as the weight of the thread, but that is small enough to be ignored).
d) With the object still hanging from the spring balance, lower it slowly into the graduated cylinder to the point that it is completely submerged. DO NOT let it touch the bottom of the cylinder. Note two things: a) the reading on the spring balance, and b) the new reading of the volume of the water in the cylinder.
e) Take the object out, and if necessary add a little water to bring its volume back to the level it was at in step (a).
f) Repeat steps (b) through (e) for all of the objects.
g) Create a table like the one below, and fill it out.
| Object | Weight in grams before being submerged | Weight in grams after being submerged | Difference in weight before and after being submerged | Volume of the object, in milliliters* |
| Bolt | ||||
| Piece of chalk | ||||
| etc. |
*This is the difference between the levels of water in the cylinder before and after the object is submerged.
Answer these questions:
1) What are the variables in this experiment?
2) What is the relationship between the decrease in weight of the object (in grams) and its volume (in milliliters)?
3) The theory of buoyancy states that an object which is submerged in water will experience an upward force which increases with the volume of the object which is submerged. Does your experiment support the theory? Explain.
Teaching Guidelines: Investigating Buoyancy
Math Topics: Measurement (weight, volume), Algebra (variables, patterns and functions)
Students should find that the difference in weight of the object, in grams, is equal in each case to the volume of the object, in milliliters. What is most important is that they realize that the buoyant force on an object increases as its volume increases. You may also wish to take this farther and ask students to decide if this is true: “The buoyant force on an object is equal to the weight of the amount of water that has the same volume as the object.” Make sure that students know that one milliliter of water weighs one gram.
As an extension, once students have found that their experimental data supports the theory of buoyancy, ask them to investigate what happens if the object is only partially submerged in water. They should find that the same relationship holds true, which means that the buoyant force depends on how much of the object is below the surface of the water. This is especially important because it explains why some objects float: they submerge only to the degree that the amount of buoyant force on the part that is submerged is equal to the weight of the entire object.
Measurement (speed, conversion)
The speed of sound in water is much faster than in air: around 1,500 meters/second, compared to 340 meters per second. Low frequency sounds, such as are made by whales, can travel great distances underwater. If a
blue whale in the Pacific makes a sound that travels 3,000 miles across the ocean, how long does the sound take to make that journey?
