• Ratio (explicit)
• Pattern (explicit)
• Variable (implicit)

• Can apply the problem-solving strategy “look for a pattern”
• Can solve multi-step problems
• Can solve equations of the form ax = b

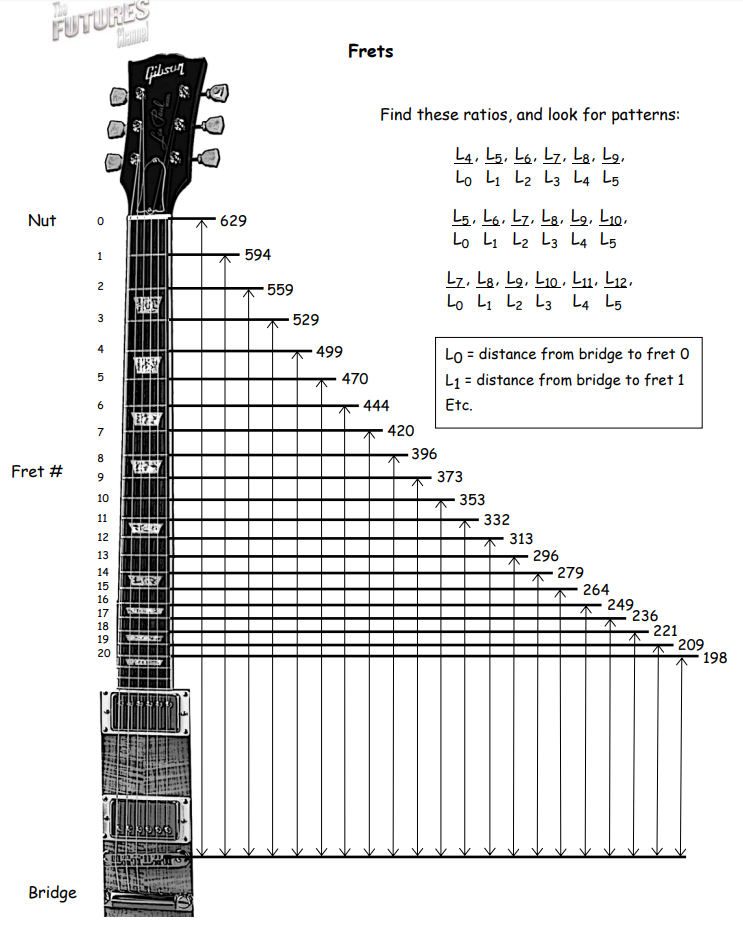
Procedure: Distribute the handout “Frets” to students working individually or in teams of two. Ensure that they understand what the diagram represents, and ask them to see what patterns they can find in the ratios indicated.

Answers: For the first set of ratios, the value is very near to 4/5. For the second set, it’s 3/4. For the third set, it’s 2/3.

Once students have completed this part of the activity and see the patterns in the ratios, pose this problem:

“Suppose you are building a guitar where the distance from the bridge to the nut is 1000 millimeters. Use what you have discovered about the ratios of the fret positions to determine the locations of each of the first 12 frets.”

Let students work for a while without help; for students who seem to be making no progress, you may wish to suggest that they first find the location of fret 5, then use that information to find the position of fret 2, and continue in that fashion.

Answer: Since the ratio of L0 to L5 should be 3/4, then the position of fret 5 would be found by solving the proportion L5/L0 = 3/4, giving L5 = 750 millimeters. Then use the fact that the ratio of L1 to L5 should be 4/5 to find L1. Continue in this fashion to find L6, L2, L7, L3, L8, L4, and L9. L10, L11, and L12 can then be computed from L5, L6, and L7.

As a quick method of checking answers, the distance to fret 12 should be between 490 and 510 millimeters.

Explain to students that this method of calculation gives approximate, not exact, fret positions, but it should help them to see that there are mathematic relationships among notes in a scale.

Alternatively, you may wish to pose this simpler problem:

“Suppose you are building a guitar in which the distance from the bridge to the nut is 1000 millimeters. Use what you have discovered about the ratios of the fret positions to determine the location of the 12th fret.”

The solution in this case is to first find the position of the 7th fret (which the pattern indicates is 2/3 of the length of the string), and then find the position of the fret that is 5 positions above that one (using the fact that the pattern indicates that moving up 5 frets shortens the distance by a factor of 3/4). The combination of the two ratios (first 2/3, then 3/4 of that result) yields a 12th fret ratio of 1/2 of the full string length, or 500 millimeters.