Mathematics
Grade Levels: 6th Grade, 7th Grade, 8th Grade, 9th Grade,
Topics: AlgebraRatios and Proportions
Common Core State Standard: 6.RP.3, 7.RP.1, 8.EE.5, 8.SP.2, S-IC.2,
Concepts:
Mathematics (grades 6-7 – Ratios and Proportions):
• Ratio (explicit)
• Rate (explicit)
• Extrapolation (implicit)
Mathematics (grades 8-9 – Algebra):
• Function (explicit)
• Independent variable (explicit)
• Dependent variable (explicit)
• Linear Function (explicit)
• Slope (explicit)
• Extrapolation (implicit)
• Domain (implicit)
Knowledge and Skills:
Mathematics (grades 6-7 – Ratios and Proportions):
• Can convert a ratio to a rate.
• Can use proportional thinking to solve rate problems.
Mathematics (grades 8-9 – Algebra):
• Can find the slope of a linear function
• Can solve equations of the form ax = b
Lesson:
Procedure (Grades 6-7, ratios and proportions):
Distribute the handout and discuss as needed to ensure that students understand how the applied force causes a deflection, that deflection can be measured as an angle, and what the data in the table means. Explain to students that each row in the table could be represented as a ratio of deflection to force (reviewing the meaning of ratio as needed), and have students write out those ratios, working individually.
Have students work in teams for 5-10 minutes on the task of determining a strategy for solving the problem. Share responses and elicit or present the strategy of using the data to determine how much deflection would be produced by a force of 1 pound, then multiplying to find the deflection for 6 or 8 pounds. Explain that a ratio in which the second number is “1” is called a rate, so what you want the students to do is determine the rate of deflection.
Give examples of other rates, and explain that rates are usually described using the word per, meaning for each (e.g., 10 miles per hour, $1.50 per pound, etc.).
Explain that the simplest way to convert a ratio to a rate is to divide the second number into the first (the denominator into the numerator if the ratio is in fraction form). Have students do this in teams, and to use the resulting data to answer the question.
When students compute the rates, they should get these answers:
| Force | Deflection | Rate (degree per pound) |
| 2 pounds | 0.30º | 0.15 |
| 3 pounds | 0.44º | 0.1466… |
| 4 pounds | 0.6º | 0.15 |
| 5 pounds | 0.76º | 0.152 |
As each team completes this computation, ask them to decide what rate to use in order to determine the deflection for 6 pounds, and to explain their decision to you. Guide students as needed to observe that all rates are very close to the value of 0.15, and in fact if all rates are rounded to the nearest tenth of a degree they all come out to be 0.15, so that 0.15 is a reasonable value for the rate to be used in computing the deflection at 6 and 8 pounds.
Ask teams to work out how to use the rate of .15 degrees per pound to find the deflection at 6 and 8 pounds, and again guide them as necessary to use proportional thinking to determine that if the deflection is .15 degrees for each pound, then to find the deflection for 6 pounds they should simply multiply by 6. This will yield deflection values of 0.9º for 6 pounds and 1.2º for 8 pounds of force.
Discuss the final question as a class, guiding students to the conclusion that data in the range of a few pounds probably does not allow a good prediction of what would happen in the range of a thousand pounds, which corresponds to the common sense observation that if you applied 1,000 pounds of force to the fork, it would probably break.
Procedure (Grades 8-9, algebra):
Distribute the handout and discuss as needed to ensure that students understand how applied force causes a deflection, that deflection can be measured as an angle, and what the data in the table means. Ask students what strategy they could use to predict the deflection at 6 and 8 pounds, and guide the discussion to the recognition that the table shown could be viewed as a function table, in which the force is the independent variable and deflection is the dependent variable. (Review meanings of function, independent variable and dependent variable as needed.)
Have students work in teams to graph the data, assisting them in determining appropriate scales for the x and y axes as needed.
Have teams verify their graphs against the graph on the next sheet (which may be copied onto a transparency for use with overhead, if you wish). Then draw in the line connecting the points and explain or review the fact that a function whose points line up in that way is called a linear function, and if the line goes through the origin (as this one does, shown by extending the line) then such a function may be represented by the equation y = ax.
Explain (or review as needed) how the value “a” is calculated as the slope of the graph. Have teams calculate the slope (0.15) using two of the points (0,0), (4,0.6) and (8,1.2) and then use the equation y = 0.15x to find the deflection for forces of 6 and 8 pounds (0.9º and 1.2º).
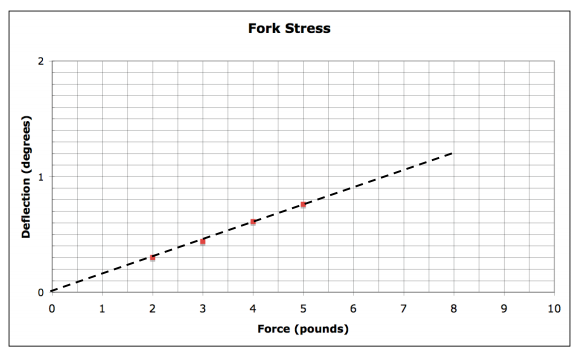
Discuss the final question as a class, guiding students to the conclusion that data in the range of a few pounds probably does not allow a good prediction of what would happen in the range of a thousand pounds, which corresponds to the common sense observation that if you applied 1,000 pounds of force to the fork, it would probably break.
Frame Stress
The diagram below shows that when a force is applied to the frame of a bicycle (while the rear of the frame is held in a fixed position), the frame bends slightly. When force is applied to something to see how it affects its shape, it is often called stress. The amount of bending can be measured as an angle, and is called the deflection.
Note that the defection in the diagram is exaggerated to make it easier to illustrate.

This table shows the amount of deflection, in degrees, that resulted from various amounts of force:
| Force | Deflection |
| 2 pounds | 0.30º |
| 3 pounds | 0.44º |
| 4 pounds | 0.61º |
| 5 pounds | 0.76º |
1) What deflection would you expect for a force of 6 pounds? 8 pounds?
2) Do you think you could use the table to predict the deflection for a force of 1000 pounds? Explain.
