Mathematics
Grade Levels: 8th Grade, 9th Grade, 10th Grade, 11th Grade, 12th Grade,
Topics: GeometryProblem Solving
Common Core State Standard: 8.G.7, 8.G.9,
Concepts:
• right triangle
• hypotenuse
• Understands and can apply the Pythgagorean theorem.
• Can solve an algebraic equation involving squared quantities
Lesson:
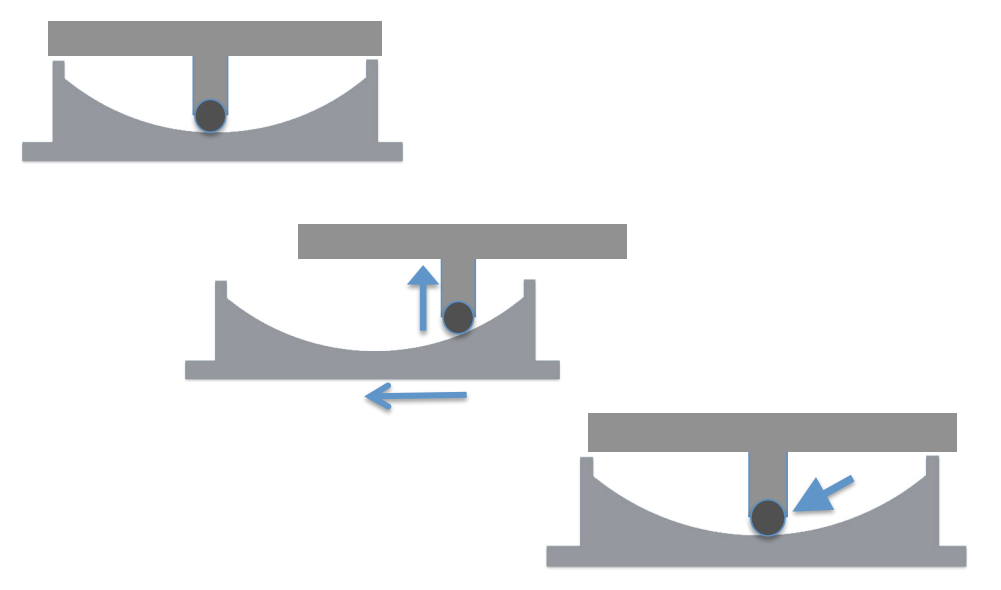
The diagrams below show the main features of an earthquake base isolator. The black circular shape represents a spherical bearing. As the center diagram illustrates, when the lower section of the isolator moves sideways, as it might during an earthquake, the top of the isolator (on which the building rests) slides upwards. The third diagram illustrates how the force of gravity will then pull the top section of the isolator—and the building—back down into a stable position in the lower section.
In designing an isolator, one of the questions an engineer would need to answer is, “If the ground moves sideways by a certain amount, how far up would the building move?” The question is represented in the simplified diagram below:
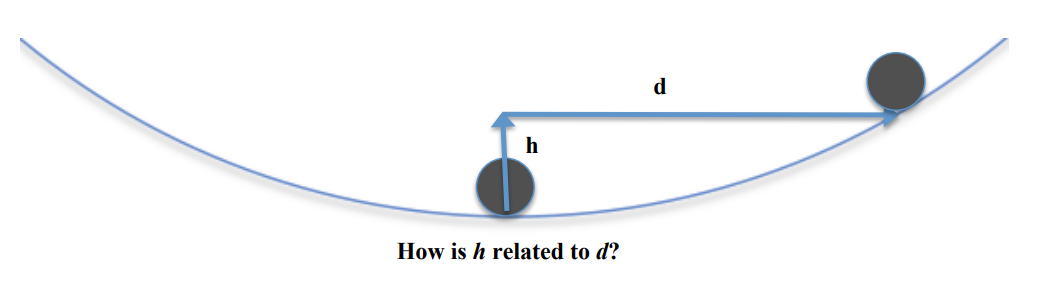
This problem can be solved with algebra if the curve thought of as part of a circle with a radius R, as shown below.

In this case, the relationship between d, h, and R can be represented by this equation
(R – h)2 + d2 = R2
Answer one or both of these questions:
1) Explain the reasoning that leads to the given equation.
2) Find h if R = 80 cm and d = 20 cm.
Answer:
2.54cm
