Mathematics
Grade Levels: 6th Grade, 7th Grade, 8th Grade,
Topics: DecimalsFractionsMeasurement (length)PercentsGeometry (polygons)Geometry (Circles)GeometryMeasurement (general)ProbabilityStatisticsAlgebraScientific NotationVariablesExpressions and EquationsFunctions and Relations
Common Core State Standard: 4.NF.3a, 4.NF.4, 4.MD.2, 4.MD.3, 6.RP.3d, 6.G.1, 6.SP.5c, 7.G.6, 8.EE.4, A-CED.2,
Download the Teacher Guide PDF
Lesson:
Background: In order to compete in a crowded marketplace, a new style of sunglasses must combine high fashion with
good fit, strong construction with light materials, protection of the eye with an eye on the bottom line. The
designer of such a product needs to be 50% artist, 50% engineer, and 100% savvy businessperson.
Curriculum Connections:
Fractions
Suppose that 1/3 of the population of a given city buys sunglasses and 1/8 of those people usually buy a certain style of sunglasses. What fraction of the total city population buys that style of sunglasses?
Measure several of the dimensions of a pair of sunglasses in inches and fractions of an inch (for example, 3-5/16 inches). If you wanted to make a pair of sunglasses that was exactly 2/3 the size of the pair that you measured, what would its dimensions be?
Decimals
Even small changes in the design of a product can make big changes in the amount of material used in manufacturing the product. If a change in design saves 0.32 grams of plastic per pair of sunglasses, how much plastic would be saved over 5 years if 25,000 pairs of sunglasses were made every year?
Decimals, Measurement (length)
Suppose that a style of sunglasses designed in the United States is going to be manufactured in Europe. The machinists who manufacture the sunglasses in the United States still use inches and decimal fractions of inches. Since machinists in Europe use the metric system, the design dimensions will have to be changed. Convert each of these measurements to millimeters.
| Part measured | Measurement (in inches) | Measurement (in millimeters) |
| Lens size and shape | 2.5 inches by 2 inches (rectangular) | |
| Temple-to-ear | 7.12 inches | |
| Pupil-to-pupil | 2.84 inches |
Percents
Suppose one type of sunglasses transmits 30% of the visible light that strikes them. If you wore two pair of these sunglasses, one in front of the other, what percent of the light that strikes the outside pair would reach your eye?
Some designs are more difficult to manufacture than others, which may mean that there are more rejects from the manufacturing process. (Rejects are products that do not pass inspection and cannot be sold.) Suppose a company sets a limit of 7% rejects on manufacturing. If there are 1,243 rejects out of 16,000 sunglasses manufactured, have they exceeded the limit?
This table shows the results of a survey on product preferences for four different styles of sunglasses. Forty-one percent of those surveyed chose not to buy any of the styles shown.
Suppose these results are applied to a group of 50,000 buyers of sunglasses. Calculate how many people would buy each style, and then determine which style would be most profitable.
| Style A | Style B | Style C | Style D | |
| Percent of people who prefer the style | 12% | 8% | 24% | 15% |
| Number of people out of 50,000 who would buy the style | ||||
| Profit on style per pair sold | $10.00 | $12.00 | $4.00 | $8.50 |
| Total profit on style per 50,000 people |
Geometry (polygons, ellipses)
Find the surface area of each proposed lens. If the lenses are to be 1.5 millimeters thick, what would their volumes be?
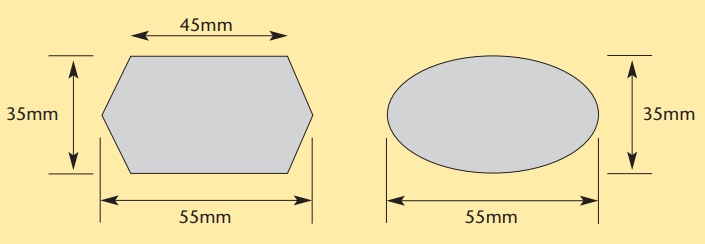
Geometry (circles)
What is the area of a circular glass or plastic lens with a radius of 2.5 centimeters? Assume that the lens will fit in a wire frame. What length of wire would be needed to enclose each lens?
Geometry, Measurement
Draw a pair of sunglasses. Try using shapes such as ovals, hexagons, and rectangles for your lenses. When you have a rough design you like, draw the sunglasses accurately, with the measurements indicated on the drawing. Make a scale drawing showing both a front and side view. Use colors for the frame and the lenses as you wish.
Get a pair of sunglasses, and use mathematical language to describe them as completely and as exactly as you can. The object is to be able to write a description that is complete enough to make it possible for someone else
to draw the sunglasses without having seen them or a picture of them. Thus the description should include the geometric shapes seen, how they are connected to each other and the measurements of all dimensions and angles.
Statistics
Bring in several pairs of sunglasses and show them to several students, asking each of them to choose a favorite pair. Keep track of the responses and prepare a report presenting the results graphically.
How would you decide whether or not to use different dimensions for girls’ sunglasses than for boys’ sunglasses for a certain age group?
Measure the temple-to-ear and pupil-to-pupil distance for each person in a group. Record your data in a table. When all the groups have finished, use all the data collected to find the mean, median, and range for each of the two measurements.
Probability
Suppose that you ask 5 teenagers in a certain city whether or not they like a certain frame style and three of them say they do. Do you think it would be safe to say that 60% of the teenagers in the city would like that style? Why or why not?
Here’s one way to find out: Assume that only 40% of the teenagers in the city actually like that style. What is the probability that if you choose 5 of those teenagers at random, three of them will happen to be part of that 40% and will say that they like that style?
Measurement, Scientific Notation
All electromagnetic radiation, including light, radio waves, x-rays, and so on, is characterized by its wavelength. The wavelength of light is extremely short and is measured in nanometers, where 1 nanometer = 10-6 millimeters.
One type of light that sunglasses should block completely is called “Ultraviolet A”. It has wavelengths in the range of 320 to 400 nanometers, whereas visible light has wavelengths in the range of 400 to 700 nanometers.
Convert each of these wavelengths to their equivalent in millimeters, expressed in standard scientific notation.
Algebra (variables)
● All dimensions
● Surface area of lenses
● Weight of the lenses
● Characteristics of the lens material (for example, its density)
● How much light is transmitted through the lenses
● Amount of material required to make the frames for one pair
● Cost of manufacture, per pair
● Price
Algebra (expressions, equations)
Suppose a manufacturer sells sunglasses to department stores at a price of $10.00 each, and each pair of sunglasses costs $2.48 to manufacture. If x represents the number of pairs of sunglasses sold in a year, write an expression that stands for the amount of profit (difference between price and manufacturing cost) per year on those sunglasses.
Now suppose that the company spent $220,000 to design those sunglasses and prepare to manufacture them, and also that the company has decided to spend $750,000 per year in advertising for those sunglasses. How many pairs of sunglasses would the company have to sell in the first year in order to recover its initial costs?
Algebra (functions and relations)
This table shows how the thickness of the lens of one kind of material affects the percent of visible light that is transmitted by that material.
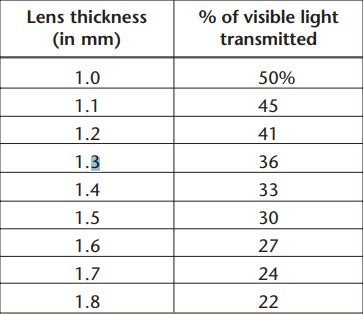
Identify the variables, and state which is independent and which is dependent. Then plot these numbers in an x-y coordinate system.
Is this a linear function? How do you know?
What transmission percent would you expect for a thickness of 1.9 mm? 0.9 mm? 2.5 mm?
