· Can multiply matrices

Procedure: This project should be done by students individually or in teams of two.

Students should understand how matrix multiplication is done prior to beginning this project.

Distribute the handout and discuss it.

Tell students that they are being asked to explore this new technique of planning crop rotations.

For example, what happens if the “new crop arrangement” is multiplied again by the same rotation matrix? Do rotation matrices have to have only 1’s and 0’s as elements? How many workable rotation matrices can be found? What do they have in common?

Tell students that part of their assignment is that they clearly explain the results of their investigations. (You may choose to have these explanations made orally or in writing.)

As an extension of the activity, students can be asked to investigate rotation matrices for crop arrangements of different sizes (e.g., 3 x 2, or 4 x 4).

Give students a schedule for working on the assignment and a due date.

FARMER’S FRIENDS CONSULTANTS

(Draft of paper for the World Farm Journal)

Crop Rotation

One of the important techniques of modern agriculture is rotation of crops.

Another technique that is gaining growing acceptance is placement of different kinds of crops in adjacent fields, which in some cases seems to help in pest control.

Thus if a farmer has twelve fields, and three different crops, in two consecutive years he might want to have them arranged as follows:

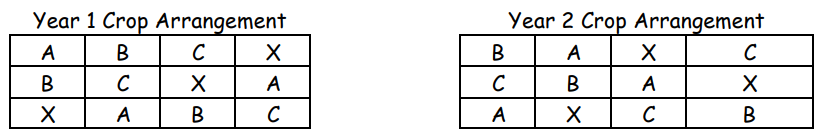
(Note: “X” means no crop at all, allowing a field to “rest” for a year)

If you study the above two arrangements carefully, you will see that no field has the same crop for two years in a row and no two adjacent fields ever have the same crop.

It would be helpful to farmers if they had an easy way to determine how to rotate. One approach to this problem is to use the mathematical technique of matrix multiplication.

Observe the results of multiplying the “Year 1” matrix above as follows:

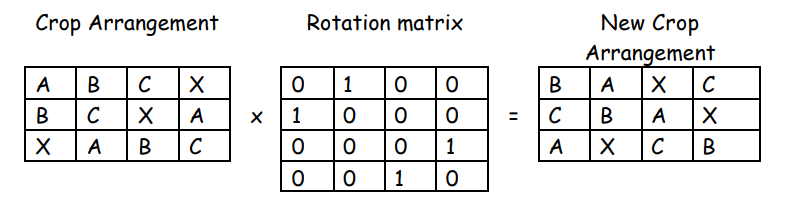
This new crop arrangement is identical to the “Year 2” crop arrangement above.

In using this technique, there are a few things that one should keep in mind:

Would you please finish this up for me—we’ll publish it under both of our names. Investigate what happens if you keep multiplying by the same crop rotation matrix, and look into what other crop rotation matrices might work. Are there any rules for creating crop rotation matrices? Eventually I think this might lead to a computer program that will make this task a little easier for farmers.

Hector