Background: There are over 84 million acres of national parks in the United States, all created based on the precedent of the very first state park, Yosemite, created by an act of Congress in 1864. Keeping those parks naturally
beautiful while accommodating over 400 million visits a year requires the design and construction of durable man-made structures and facilities which blend naturally into the scenery. There may be no more challenging or rewarding task for a landscape architect or civil engineer.

Fractions, Ratios

Make a scale drawing of a part of your school grounds, showing the position of trees, playground equipment, etc. Use a scale of 1/8 in = 1 ft.

Percents

Choose three states which have national parks, and find out the area of each state and the total area of national parks that exist in each state. What percent of each state is set aside as a national park. What percent of the area of all three states is set aside? Can you add the percents for each of the three states to find the percent of all three states? Explain.

Decimals, Measurement, Ratios

This is a map of sights to see in a national park. Draw in a set of trails that allow campers to hike from any campsite to any of the sights, and from each of the sights to another sight without having to go through campgrounds. Then use the scale of the map to determine the length of each trail and the total length of all trails, to the nearest 0.05 miles.

Ratios, Measurement: Area, Geometry: Polygons

The space below has an area of 5,120 square feet. Divide it into 5 campgrounds of 1,024 square feet each.

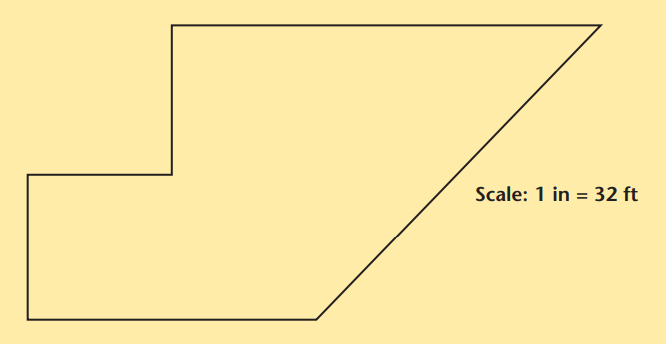
Percents

In order to evaluate the impact of visitors, you have been asked to measure the relative populations of various species of wildflowers in a potential camping area, prior to construction. In a 2-acre area you find 57 blue columbines, 23 purple deadnettles, 42 pink evening primroses, and 13 lady’s slippers. Find the percent of total wildflower population for each species.

Ratios

Campgrounds need to be built on relatively flat land. Suppose that the requirement is that the slope is less than 1 foot of rise or drop for 15 feet of travel in any direction. If the slope of a certain area is measured as 3 feet of drop for 42 feet of travel in a certain direction, could it be suitable for a campground?

Statistics, Probability

This chart shows the number of campers per year at Canyon de Chelly park.

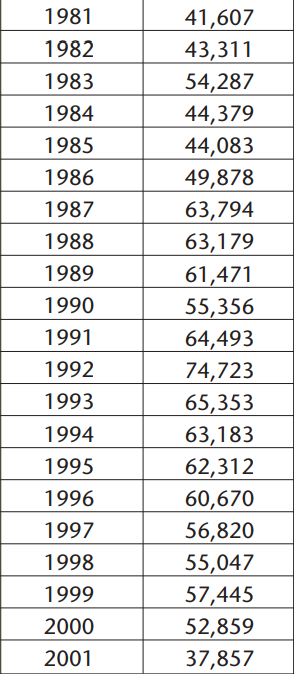
What would you estimate as the probability that the number of overnight campers in the year 2005 will be less than 50,000? More than 70,000?

Trigonometry

A trail climbs up the hillside at an average angle of 8 degrees. If the trail is 1,350 feet long, what is the altitude difference between the start and end of the trail?

The Campground

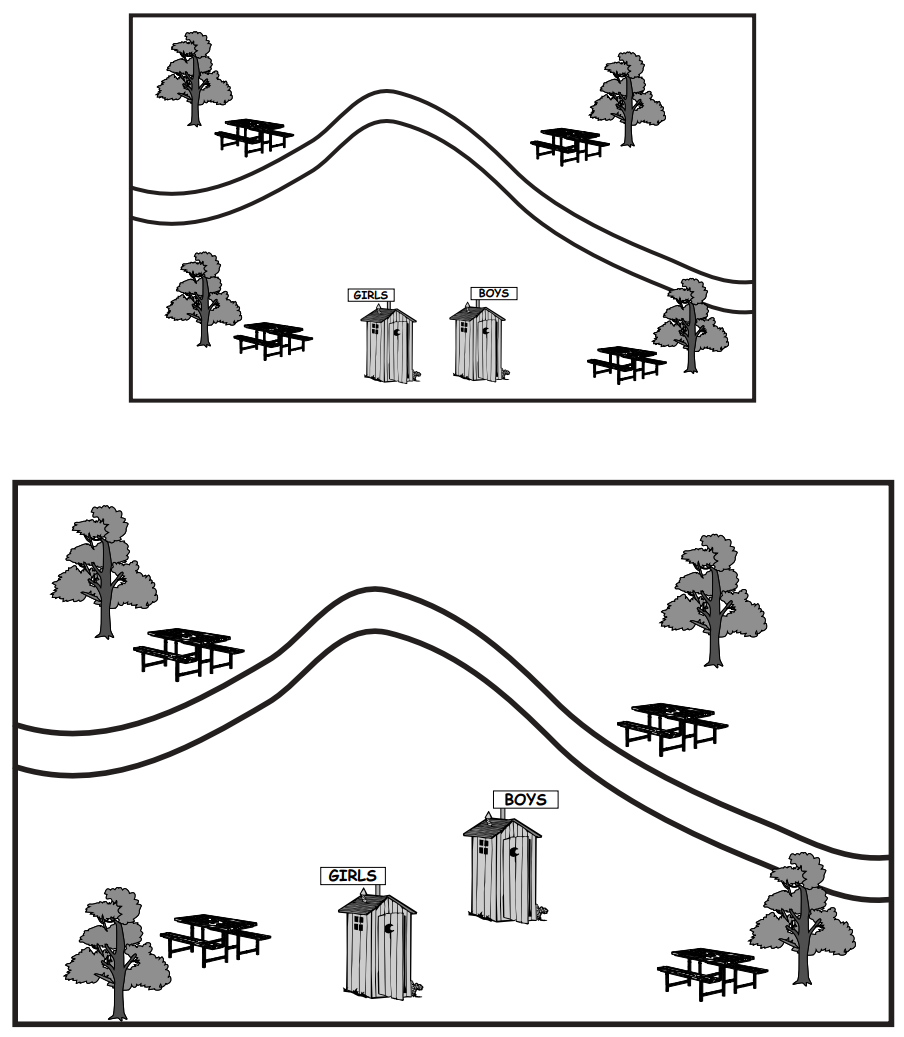
The campground map at the bottom is supposed to be a copy of the map at the top, only larger in the ratio of 3:2. But there are three items in the bottom map that are not in the right position. Can you tell what they are and show exactly where they should be?

Teaching Guidelines: The Campground
Math Topics: Ratios, Measurement (length)

Procedure: Students can do this activity individually or in teams of two. Each student or team will need a centimeter ruler.

Hand out the activity sheet and discuss the two maps. Explain that one map is supposed to be an
exact copy of the other map, only larger in the ratio of 3:2. As a class activity, have all students measure the lengths and widths of the two maps and verify that they are in the correct ratio.

Explain that there are three items in the bottom map which are not in the correct position. Tell students that their assignment is to find out which items those are, and to figure out where they should be. Ensure that they understand the problem, but do not allow discussion of solutions yet. Once all students do understand the problem, have them start trying to solve it.

Circulate as students work on the problem. If needed, you may give individual students or teams the hint that they could measure the distance of all objects from two of the corners of the maps. (The distances should be measured in millimeters as this makes it easiest to compare them.)

Once students discover the three items that are out of place (the tree at bottom left, the boys’ outhouse, and the picnic table at upper right), they will need to carefully measure the positions of those items on the smaller map (by measuring the distance to any two corners), and then determine the corresponding distances on the larger map using the ratio of 3:2.

In addition to improving students’ grasp of the concept of ratio and their ability to work with ratios, students will gain some experience with the idea that the position of any object on a two dimensional surface can be specified by making two measurements.