· Factor
· Multiple
· Diameter

· Can apply the strategy of “make a model”
· Can find two factors of a given number

(for each team):
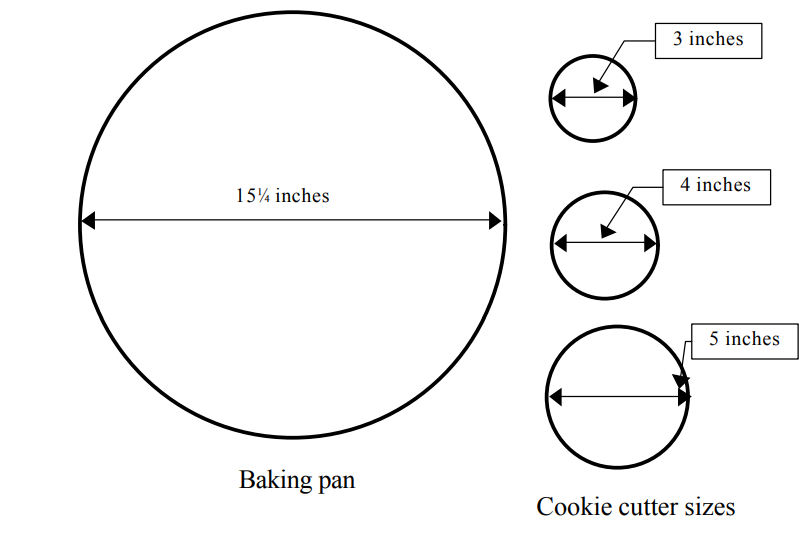
· one 15½-inch diameter “baking sheet” (cut from construction paper)
· twenty-five 3-inch “cookies”
· twenty 4-inch “cookies”
· ten 5-inch “cookies”

(You may choose to make this a “math and art” activity by having students make and decorate their own batches of 3-inch, 4-inch and 5-inch cookies.)

Procedure: This activity is best done in groups of two, three or four students.

1. Once you have distributed the activity sheet, ask a student to read what it says.

2. Discuss whether or not this is a “problem”. Why would one size cookie be better than another size? (Because you could fit a batch of cookies on the baking sheet better.)

3. Ask students what they could do to decide which size cookies to make. Discuss the various problem solving strategies, and help the students to see that “making a model” is a good strategy for this problem.

4. Bring out your construction paper baking sheets and cookies (or have the students make their own cookies).

5. As students try to arrange the cookies on the sheet, they should discover arrangements whereby both the 3-inch and 5-inch cookies fit without much wasted space. The 4-inch cookies will not fit well on the sheet. This is because fifteen is a multiple of three and five, and therefore five 3-inch cookies and three 5-inch cookies fit well on the 15½ inch diameters of the circle without much wasted space at the outside of the cookie sheet. 4- inch cookies leave more wasted space with such an arrangement.

6. Once the students have arranged the cookies as above, ask them what they could say to describe the way the cookies are placed on the sheet. (For example: “The cookies are arranged on diameter lines,” “the cookies are in rows that get longer and then shorter”, “the arrangement is symmetric,” etc.)

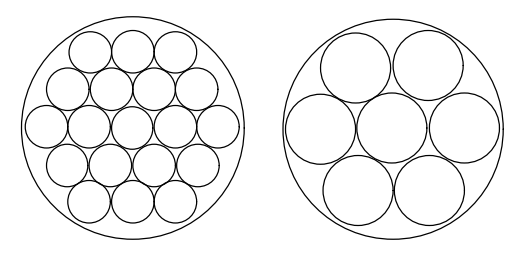
7. As a class discussion, ask students why they think that 3 inch and 5 inch cookies fit well, but 4 inch circles did not. Help them to see that the diameter is related to how many cookies fit, and note that the diameter is just a little over 15 inches.

Write down “5”, “3”, and “15” on one part of the board, and “4”on another part, and ask students if they can see any connection between the 5, 3, and 15 that does not apply to the 4. Lead students to the idea of factors and/or multiples, and the realization that the solution to their problem lies in finding the factors of 15. Then ask students to use what they have learned to decide what sizes of cookies would work best on a 20-inch diameter baking sheet (2-inch, 4-inch, and 5-inch).

Cookies

Imagine that you have decided to make some cookies.

You are going to bake the cookies on a circular baking sheet. But first you have to decide how big to make the cookies.

Your baking sheet is 15½ inches in diameter. You have cookie cutters for 3-inch, 4-inch and 5-inch cookies.

Which cookie cutter should you use? Why?