Mathematics
Grade Levels: 7th Grade, 8th Grade, 9th Grade, 10th Grade, 11th Grade, 12th Grade,
Topics: AlgebraMeasurement (general)Ratios
Common Core State Standard: F-BF.5, F-LE.3,
Concepts:
- Measurement (speed, frequency and wavelength)
- Algebra (using formulas)
- Logarithms
- Ratios
Lesson:
Background: Musicians, vocalists, composers and conductors devote much of their lives to the creation of what they consider to be ideal listening experiences. Instruments are thoughtfully chosen for certain parts because of
their quality of sound; voices are painstakingly trained to hit pitches perfectly over a wide range; the tone, volume and duration of every note played by every instrument in a 2-hour concerto has been carefully specified.
The result of this devotion is, often, a live performance in a concert hall. And, in fact, the hall itself is an instrument, because its design and construction determine how well the audience hears what the musicians
are playing. Think of an acoustician as the person who designs and tunes that instrument, and you will have a good idea of the purposes and products of this very interesting career.
Curriculum Connection:
Measurement (speed, frequency and wavelength), Algebra (using formulas)
Sound is a vibration of air. Its pitch is determined by how fast the vibration takes place, which is called frequency.
As the vibration travels through the air, it creates alternating regions of slightly higher and slightly lower density;
the distance from one region of high density to the next is the wavelength of the sound.
Wavelength and frequency are related by this formula: λ vν = c*
λ = wavelength, in meters
ν = frequency, in cycles per second
c = speed, in meters per second
The speed of sound, c, varies depending on the temperature of the air through which it is traveling and other factors, but is usually approximately 330 meters per second. Find the wavelengths of these sounds:
| The lowest frequency that a human ear can hear | 20 cycles per second |
| Lowest note on a piano | 27 1/2 cycles per second |
| The “A” above middle C on a piano | 440 cycles per second |
| Highest frequency of the human voice | 1,200 cycles per second |
| Highest note on a piano | 3,520 cycles per second |
| Highest frequency that a human ear can hear | 20,000 cycles per second |
*Traditionally in mathematics and science, the wavelength of a vibration is represented by the Greek letter lambda (λ), the frequency is represented by the Greek letter nu (ν), and its speed of travel is represented by the English letter c.
Logarithms
The loudness of sound is measured in comparison to a standard intensity, which is at the threshold of human hearing.
The unit of comparison is the “Bel”, which is equal to the logarithm, base 10, of the ratio of the sound’s intensity to that standard intensity.
Thus a sound which is 100 times louder than the standard threshold intensity of sound would have a loudness of 2 Bels:
Bels=log10 ( intensity of sound being measured / intensity of threshold sound)
= log10 (100)
= 2
Generally, sound engineers use smaller units of comparison, called decibels (abbreviated dB).
dB = 10•log10 ( intensity of sound being measured / intensity of threshold sound)
A sound which is 100 times the standard threshold intensity of sound is, therefore, equal to 20 decibels.
dB = 10•log10 (100)
= 20
One way that acousticians determine the sound reflection qualities of a concert hall is to fire a gun (or pop a balloon) and then measure the amount of time it takes for the echoes of the sound to die down to a level that is 1 millionth (10-6) of the original volume of sound. Express the comparison of the original sound to that measured level in decibels.
Sometimes acousticians use a different measure, called RT30, which is the time required for echoes to die down by a factor of 30dB. What is the ratio of intensity of the original sound intensity to the RT30 sound intensity?
What would it be for RT20?
Ratios
When a single note is played on an instrument, the result is not, as you might expect, a pure vibration with the frequency of that note. In addition, vibrations at several other frequencies are produced, called overtones.
These frequencies are multiples of the original frequency, as illustrated in this chart of overtones for the piano note “A above middle C”:
| Vibration | Frequency | Ratio |
| Fundamental | 440 cycles per second | 1:1 |
| First overtone | 880 cycles per second | 2:1 |
| Second overtone | 1,320 cycles per second | 3:1 |
| Third overtone | 1,760 cycles per second | 4:1 |
| Fourth overtone | 2,200 cycles per second | 5:1 |
| etc |
The relative strengths of these overtones is different, depending on the instrument. This explains why different instruments, even when playing the same note, don’t sound exactly the same.
a) What is the frequency of the second overtone of middle C on a piano (fundamental frequency = 261.6 cycles per second)? The fifth overtone?
b) What is the frequency of the first overtone of the G above middle C on a piano (fundamental frequency = 392 cycles per second)? The third overtone?
c) Compare the answers to (a) and (b). Why do you think that these two notes sound good together?
Measurement (length, rate), Ratios
When sound comes from an instrument on the stage of a concert hall, it can reach a member of the audience in more than one way.
First, the sound goes directly from the instrument to the listener. This is the fastest route. But the sound can also be reflected off of the walls of the hall towards the listener. This always takes more time.
An important characteristic of a hall is the length of time between the moment when the listener hears a sound which has come directly from the instrument, and the moment when the listener hears the first reflected sound. This interval is called “reflection time”.
The diagrams below show two concert halls of different shape. In each concert hall, several routes of sound are shown between an instrument on the stage and the position of a listener.
For each hall, determine the amount of time required for sound to arrive to the listener along each of the routes shown. Use 330 meters per second as the figure for the speed of sound.
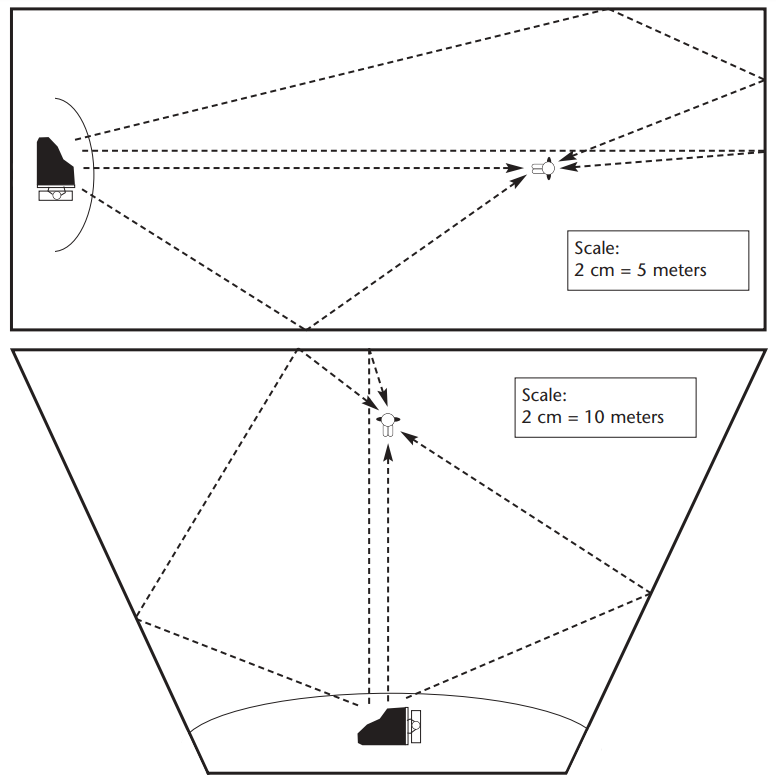
For which hall is the reflection time lower for the listener pictured? Do you think this would be true also for listeners in other positions? Experiment to find out.
Percents, Algebra (patterns and functions)
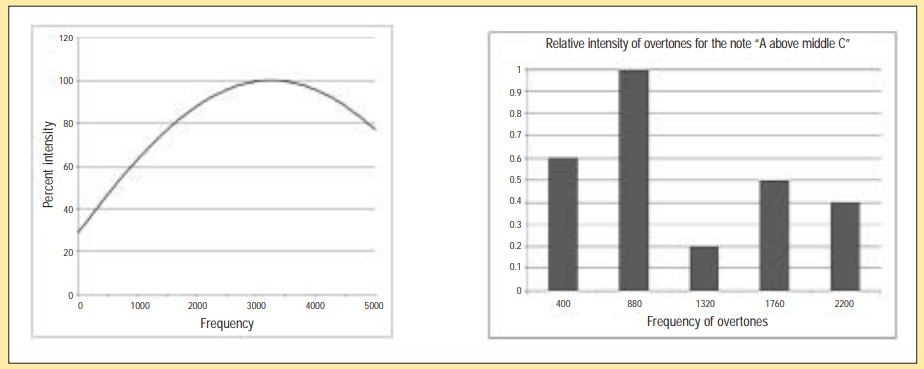
An important characteristic of a concert hall is the fidelity with which the audience can hear various frequencies. A badly designed concert hall will muffle low frequencies and exaggerate higher frequencies of music. It is also possible to dampen the higher frequencies too much, which can suppress overtones (see problem #3 above).
The graph on the left below shows what happens with frequencies of sound in a certain concert hall. For example, the graph indicates that frequencies which are around 1,000 cycles per second are dampened to 60% of their intensity.
The second graph shows the relative intensities of overtones produced by an instrument which is playing the note “A above middle C”.
Combine the information in the two graphs to produce a third graph that shows the relative intensity of overtones of the note “A above middle C” that would be heard by a listener in that concert hall.