Mathematics
Grade Levels: 2nd Grade, 3rd Grade, 4th Grade, 5th Grade, 6th Grade, 7th Grade,
Topics: ArithmeticRatios
Common Core State Standard: 3.MD.1, 6.RP.1, 6.NS.5, 6.EE.4, 7.RP.2a, 7.RP.2c, 7.NS.1,
Concepts:
Grades 2-4
• Equality
Grades 5-7
• Ratio
• Proportion
Grades 2-4
• Can add whole numbers (up to two digits)
• Optional: Can multiply single digit numbers
Grades 5-7
• Can create a ratio
• Can determine whether or not two ratios are equal
• Plastic straws
• String
• Copies of handout (if you wish, these can be done on colored construction paper)
• Rulers (for older students)
Lesson:
Procedure:
This activity can be done at various levels of difficulty.
In all cases, students should cut out the bats on the dotted lines, producing rectangles of the exact dimensions indicated. This is important because it is the size of the rectangles that determine the relative weights of the “bats”, and consequently how they should be arranged in the mobile so as to make it balanced.
For younger or less advanced students, the mobiles should be constructed so that each straw is suspended through its center point, and all straws supported by a single string in a vertical arrangement. Their task then becomes to determine how to equalize the total weight of bats suspended from each end of each straw (e.g., a 24-gram bat on one end would be balanced by four 6-gram bats, six 4-gram bats, or two 6-gram bats plus three 4-gram bats; two six-gram bats on one end would be balanced by three 4-gram bats at the other end). Thus the activity becomes a lesson in addition (or, if you wish, multiplication or division: e.g., How many 4 gram bats does it take to make 24 grams?), and an opportunity to introduce or review the concept of equality (the total weight of bats on each end of the straw are equal to each other).
For older and more advanced students, you can have students experiment to determine the proper suspension point on each straw, depending on the total weight of bats at each end. They will learn that the straws need to be supported closer to the heavier end. If the straws are light enough relative to the weight of the bats¹, then this equation will hold:
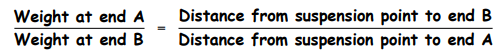
You may wish to have students experiment to discover this relationship, or to present the relationship and have students test its truth in their constructions.
More advanced students can explore what happens when some straws are suspended from the ends of other straws, rather than have all straws supported from the same string. The above equation will still hold true, but in that case the “weight at end A” would be computed as the entire weight of the straws plus bats which are being supported from end A.
¹If the straw has weight comparable to the bat cutouts, the equation won’t hold true. You may therefore wish to provide heavy construction paper or carboard stock to make the bat cutouts so as to increase the weight of the bats relative to the weight of the straws.
Bat Mobile:
There are many kinds of bats. Some are smaller, and some are bigger.
Use these patterns to make a mobile with bats. The numbers show the weight of each bat, in grams. Use math to balance your mobile.

