Mathematics
Grade Levels: 3rd Grade, 4th Grade, 5th Grade,
Topics: StatisticsGeometry (polygons)Measurement (distance, time, speed)
Common Core State Standard: 4.G.2, 5.G.3, 7.G.4, 7.G.6, G-MG.1, S-IC.1, S-MD.7,
Concepts:
• Speed
Knowledge and Skills:• Can divide a two digit number by a two digit number (distance by time)
• Can measure lengths.
• Can solve problems involving speed
• Can compute an average
• Understands and can apply the formulas “circumference = л × diameter” and “circumference = 2 × л × radius”
• Can specify defining characteristics of common polygons
• 1 stopwatch (preferred) or any watch which can be read to the nearest second (for each team)
• 1 millimeter ruler (for each team)
Lesson:
Procedure:
Arrange students into teams. Ideally, each team would have a stopwatch, so the number of stopwatches available would determine the size of the teams. If stopwatches aren’t available, make teams of 2-4 members each.
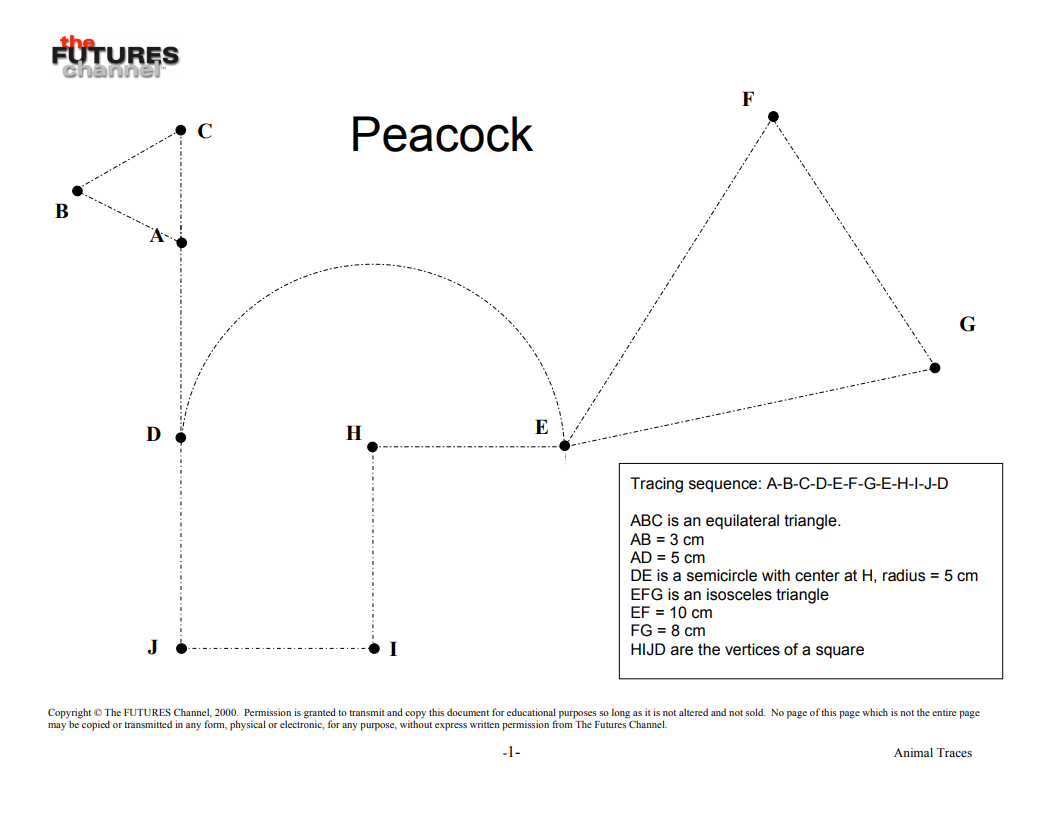
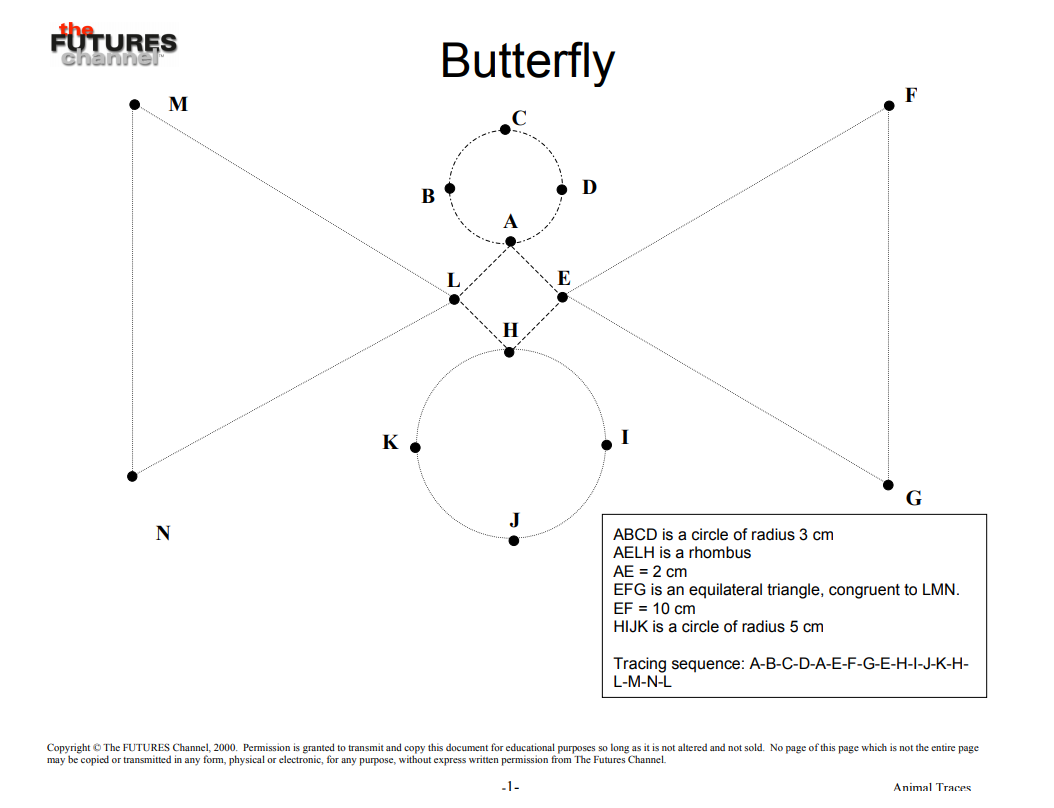
Each member of each team is to trace the outline of the peacock and the butterfly as rapidly as they can, while another team member times them.
In order for any effort to qualify, the lines drawn should at no point stray more than 1 millimeter from the dotted lines. This is to be verified after each trial, and if the drawing does not qualify the team member must try again
Once all team members have traced the shapes, each team (or, at the instructor’s discretion, each individual team member) should work out the total length of the path traced. (Students are to determine this only from the data provided on each drawing, not by measurement.) Then each team member should compute his or her speed for both shapes.
Team averages should then be computed for each shape separately and both shapes together. Awards can be made for fastest team overall, fastest team peacock, fastest team butterfly, fastest individual peacock and fastest individual butterfly.
Questions for discussion:
Based on the speeds of individual students for both shapes, does it seem that one shape is easier to trace quickly than the other? If so, what might explain that? How could you test that explanation?
Optional: Have students make up the own animal traces, for which knowledge of the characteristics of geometric shapes is required to compute the total length of the trace.