Mathematics
Grade Levels: 6th Grade, 7th Grade, 8th Grade, 9th Grade, 10th Grade, 11th Grade, 12th Grade,
Topics: AlgebraCoordinate SystemsPatternsFunctions and Relations
Common Core State Standard: A-REI.11, F-IF.2, F-IF.4, F-IF.5,
Knowledge and Skills:
· Can plot a point in a two-dimensional coordinate system, given the coordinates, or determine the coordinates of a given point
· Can find a “best-fit” equation as a model for a relationship, given a set of data points
Lesson:
Procedure: This activity is best done by students individually or in teams of two.
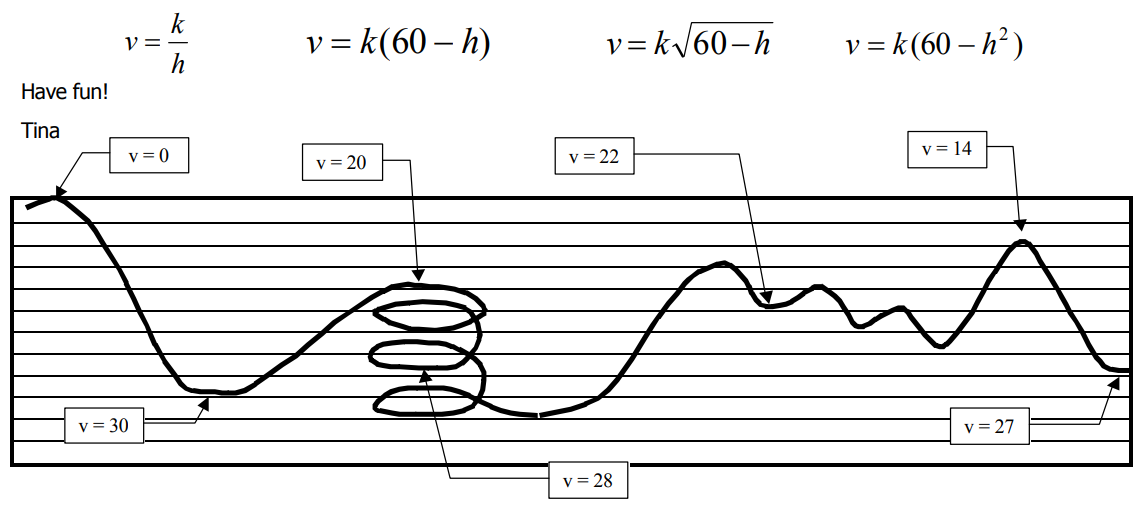
Distribute the handout and discuss the instructions. (Begin by asking students if they can explain what the diagram represents.)
The graph that students make should look something like this.
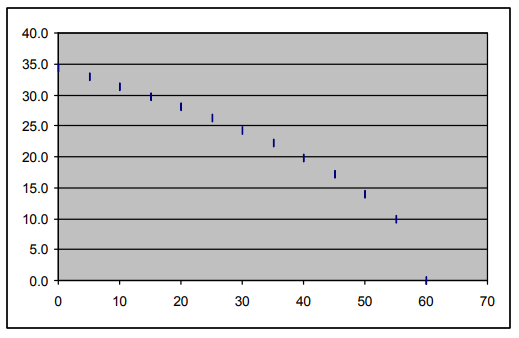
To test the given equations, students can plug in one pair of h and v values to find a value of k, then use that value to graph the equation and see how well the resulting curve matches the other data points on their graph.
Alternatively, and as a method of investigating the behavior of these equations more thoroughly, you might wish to ask students to graph a family of equations for different values of k, and in that way determine the value of k that creates a curve that most closely matches their data for each type of equation. For such an investigation, it is suggested that students use graphing calculators or spreadsheet software to create the graphs.
Air Coasters
To: Performance Analysis Chief
From: Design Team Manager
Luis, here is the data we collected on our last test run on the frictionless coaster. As usual, let’s plot the velocity versus height.
The highest point in this test run was 60 meters, and the grid lines below are 5 meters apart. Velocities are in meters per second.
In order to compare the actual performance against what we predicted, the project physicist wants you to try to match the data to one of these equations, and let him know which has the closest match, and the value of “k.”